断層モデルによる地殻変動計算プログラム
DC3D0 / DC3D
1 プログラム概要
DC3D0 / DC3D は、Okada (1992) [Bull. Seism. Soc. Am., 82, 1018-1040] の定式化に基づいて、半無限弾性体中の点震源(DC3D0)または有限矩形断層震源(DC3D)により生じる、媒質内部および地表面の任意の点における変位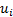 および変位微分
および変位微分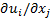 を求めるサブルーチン・パッケージです。
を求めるサブルーチン・パッケージです。
この変位微分値から、媒質中の歪み及び応力は、次式により計算することができます。
歪み 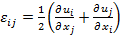
応力 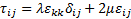 (
(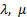 は Lame 定数)
は Lame 定数)
【参考論文】
2 ダウンロード
DC3D0とDC3Dのフォートラン・ソースコード、使用説明書、およびフローチャートは以下のリンクよりダウンロードできます。
なお、DC3D0 / DC3D の基となっているOkada (1992)の計算式の数学的背景や導出過程について興味のある方は、以下のファイルをご参照ください。
3 使用法
DC3D0
半無限弾性体中の点震源により生じる媒質内部および表面の任意の点における変位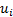 とその空間微分
とその空間微分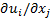 を求める。
を求める。
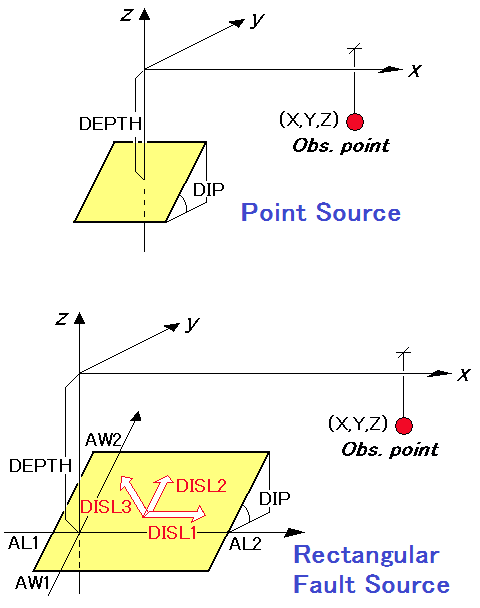
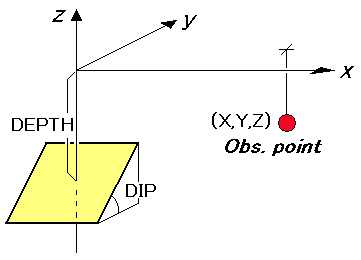
媒質はz≦0の領域を占め、x軸は断層の走行方向にとる。点震源の位置は(0,0,-DEPTH)と想定されている。
CALL DC3D0 (ALPHA, X,Y,Z, DEPTH,DIP, POT1,POT2,POT3,POT4,
UX,UY,UZ, UXX,UYX,UZX, UXY,UYY,UZY, UXZ,UYZ,UZZ, IRET)
| データ | 引数 | 型 | 呼ぶ時の内容 | 戻る時の内容 |
|---|---|---|---|---|
| 入力 | ALPHA | R*4 | 媒質定数:=(λ+μ)/(λ+2μ) | — |
| X, Y, Z | R*4 | 観測点の水平位置と深さ (Z≦0) | — | |
| DEPTH | R*4 | 点震源の深さ (DEPTH≧0) | — | |
| DIP | R*4 | 断層面の傾斜角 (deg) | — | |
| POT1, POT2 | R*4 | 左横ずれ、逆断層成分のpotency(注1) | — | |
| POT3, POT4 | R*4 | 開口、および膨張成分のpotency (注1) | — | |
| 出力 | UX, UY, UZ | R*4 | — | 変位の(x,y,z)成分(注2) |
| UXX,UYX,UZX | R*4 | — | (UX,UY,UZ)のx微分量(注2) | |
| UXY,UYY,UZY | R*4 | — | (UX,UY,UZ)のy微分量(注2) | |
| UXZ,UYZ,UZZ | R*4 | — | (UX,UY,UZ)のz微分量(注2) | |
| IRET | I | — | リターンコード =0:正常、=1:singular =2:観測点の深さZが正値 |
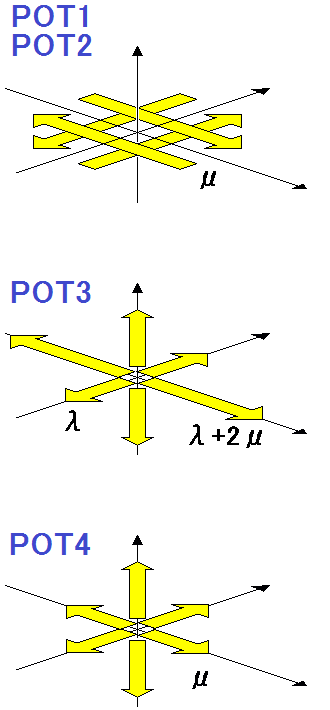
(注1)potencyの定義
- POT1,POT2については、potency=(double coupleのモーメント)/μ=LWU
- POT3については、potency=(A-nucleus の等方成分のモーメント)/λ
- POT4については、potency=(linear dipoleのモーメント)/μ
(注2)出力の単位は以下のとおり
- UX,UY,UZの単位=(potencyの単位)/(X,Y,Z,DEPTHの単位)**2
- UXX~UZZの単位=(potencyの単位)/(X,Y,Z,DEPTHの単位)**3
- potencyの単位がcm3で, X,Y,Z,DEPTHの単位がkmだった場合、両者は1.E-10cmおよび1.E-15となる。
DC3D
半無限弾性体中の有限矩形断層震源により生じる媒質内部および表面の任意の点における変位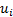 とその空間微分
とその空間微分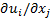 を求める。
を求める。
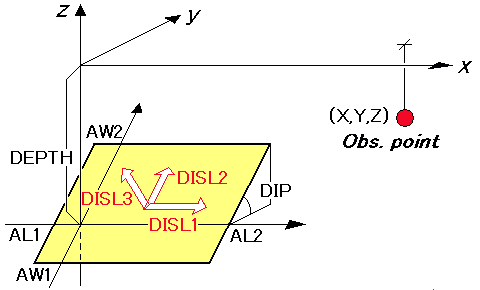
媒質はz≦0の領域を占め、x軸は断層の走行方向にとる。断層基準点の位置は(0,0,-DEPTH)と想定されており、断層面は(AL1,AL2)(AW1,AW2)の座標範囲に広がるとしている。
CALL DC3D (ALPHA, X,Y,Z, DEPTH,DIP, AL1,AL2,AW1,AW2, DISL1,DISL2,DISL3,
UX,UY,UZ, UXX,UYX,UZX, UXY,UYY,UZY, UXZ,UYZ,UZZ, IRET)
| データ | 引数 | 型 | 呼ぶ時の内容 | 戻る時の内容 |
|---|---|---|---|---|
| 入力 | ALPHA | R*4 | 媒質定数:=(λ+μ)/(λ+2μ) | — |
| X, Y, Z | R*4 | 観測点の水平位置と深さ (Z≦0) | — | |
| DEPTH | R*4 | 断層基準点の深さ (DEPTH≧0) | — | |
| DIP | R*4 | 断層面の傾斜角 (deg) | — | |
| AL1, AL2 | R*4 | 断層面の走向方向の座標範囲(注1) | — | |
| AW1, AW2 | R*4 | 断層面のdip方向の座標範囲(注1) | — | |
| DISL1 | R*4 | 左横ずれ成分の食い違い量 ⊿u1 | — | |
| DISL2 | R*4 | 逆断層成分の食い違い量 ⊿u2 | — | |
| DISL3 | R*4 | 開口成分の食い違い量 ⊿u3 | — | |
| 出力 | UX, UY, UZ | R*4 | — | 変位の(x,y,z)成分(注2) |
| UXX,UYX,UZX | R*4 | — | (UX,UY,UZ)のx微分量(注2) | |
| UXY,UYY,UZY | R*4 | — | (UX,UY,UZ)のy微分量(注2) | |
| UXZ,UYZ,UZZ | R*4 | — | (UX,UY,UZ)のz微分量(注2) | |
| IRET | I | — | リターンコード =0:正常、=1:singular =2:観測点の深さZが正値 |
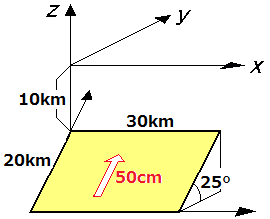
(注1)パラメータAL1,AL2,AW1,AW2の与え方の例
下図の場合、AL1=0, AL2=30, AW1=-20, AW2=0, DEPTH=10, DIP=25, DISL1=0, DISL2=50, DISL3=0 と与える。
AL1, AL2, AW1, AW2を採用することにより、下図のような不均質断層モデルを容易に構成することが可能となる。
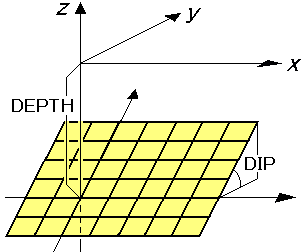
(注2)出力の単位は以下のとおり
- UX,UY,UZの単位=(DISL1~DISL3の単位)
- UXX~UZZの単位=(DISL1~DISL3の単位)/(X,Y,Z,DEPTH,AL,AWの単位)
- DISLの単位がcmで、 X,Y,Z,DEPTH,AL,AWの単位がkmだった場合、両者は1cmおよび1.E-5となる。
4 本プログラムの応用
近年、宇宙技術を用いたGPS(全地球測位システム)やSAR(合成開口レーダ)等により、地震や火山現象に伴う高精度かつ大量の地殻変動データが得られるようになってきています。
DC3D0/DC3Dはこれらの地震・火山現象をモデル化する際の標準的な道具として、また、特定の地震や火山噴火が周辺にどのような影響を及ぼすかを評価するための強力な道具として、その応用の道を拡げています。以下に、そのいくつかの例を示します。
(例1) 1986年伊豆大島噴火
1986年11月伊豆大島三原山の山腹で生じた割れ目噴火の際に、国土地理院によって全島をめぐる水準測量が実施され、複雑な上下変動の様子が実測されました。
発表されたばかりのOkada (1985)による地殻変動の理論式がこれに適用され、伊豆大島の直下に長さ15km、幅10km、開口量2mのマグマ貫入が推定されました[橋本・多田(1988), 火山, 33, S136-S144]。
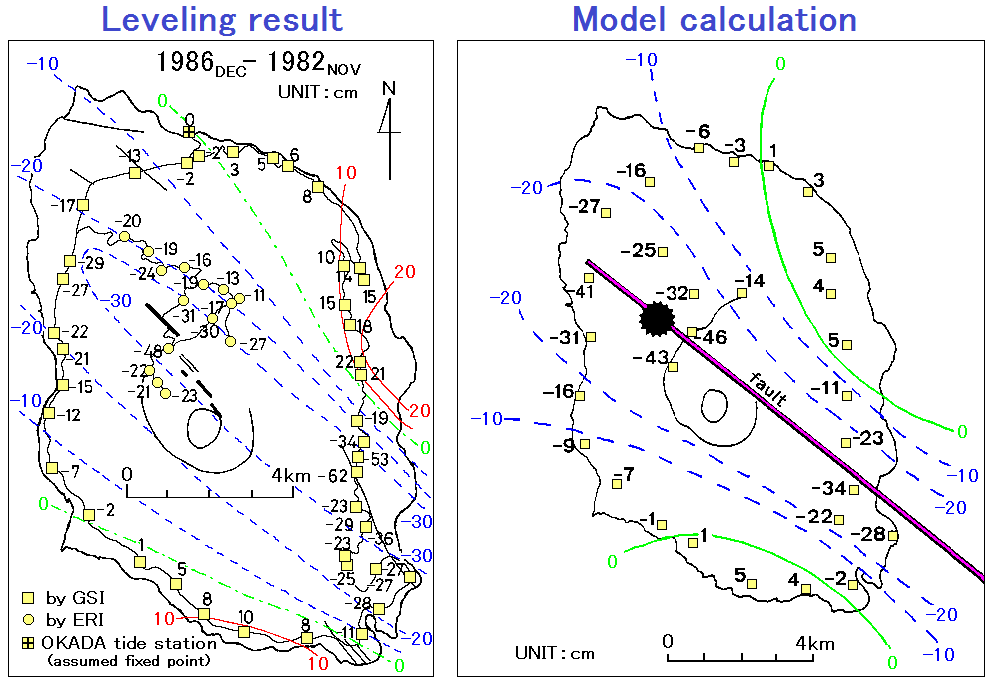
この時、防災科学技術研究所が御神火茶屋に設置していた傾斜計は噴火直前に大きな傾斜変化を記録し、これもマグマ上昇に伴う浅部への貫入としてモデル化されました[Yamamoto et al. (1991), J. Phys. Earth, 39, 165-176]。
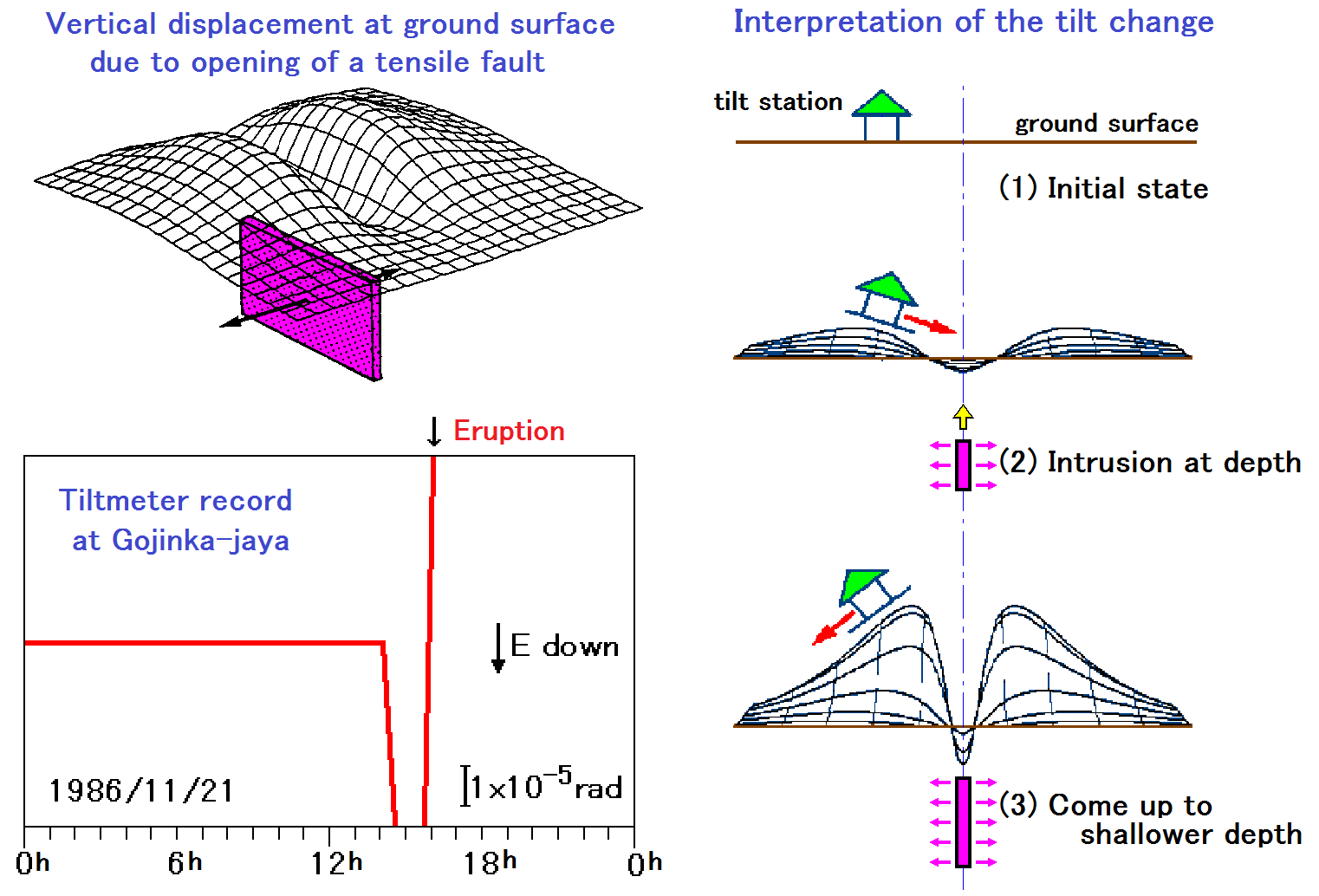
(例2) 1989年伊東沖海底噴火
伊豆半島伊東市の沖合では、1978年以来,間欠的に激しい群発地震が繰り返されてきましたが、1989年7月には海底で小規模なマグマ水蒸気爆発が起こりました。
この事件に伴って、伊豆半島東部周辺では傾斜計、体積ひずみ計、GPSなどによって大きな地殻変動が観測され、これらをOkada (1985)に基づく理論地殻変動と比較することにより、マグマ貫入の時間的な経過を含む定量的モデルが提出されました[Okada and Yamamoto (1991), J. Geophys. Res., 96, 10361-10376]。
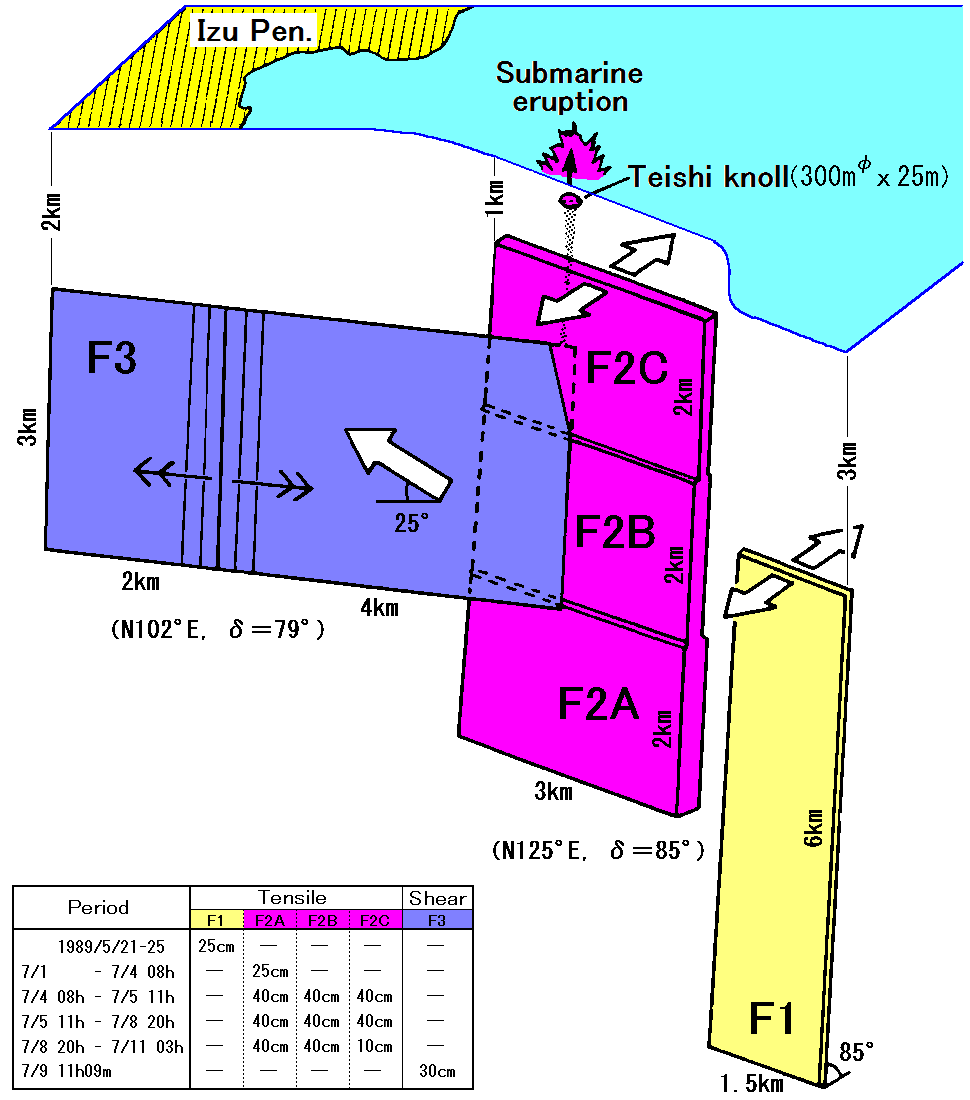
(例3) 1992年ランダース地震,1995年兵庫県南部地震
1992年6月、米国カリフォルニア州で発生したランダース地震(M7.3)に伴う地殻変動が、人工衛星ERS-1に搭載された合成開口レーダ(SAR)の画像を干渉させることにより初めて捉えられ、科学雑誌Natureの表紙を飾りました。
Okada (1985)から計算される理論的な干渉画像と比較することにより、地震断層のすべり量分布の推定などが行われました[Massonnet et al. (1993), Nature, 364, 138-142]。

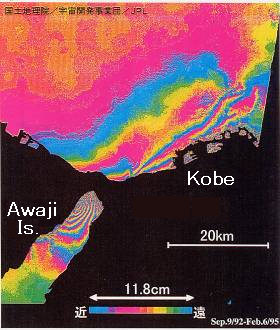
同様の手法は、その後さまざまな地震・火山活動に適用されるようになり、1995年兵庫県南部地震(M7.3)でも、干渉SARによる地殻変動パターンが地震断層モデルと整合することが確かめられました[国土地理院(2000),『地震予知連絡会30年のあゆみ』, p.20]。
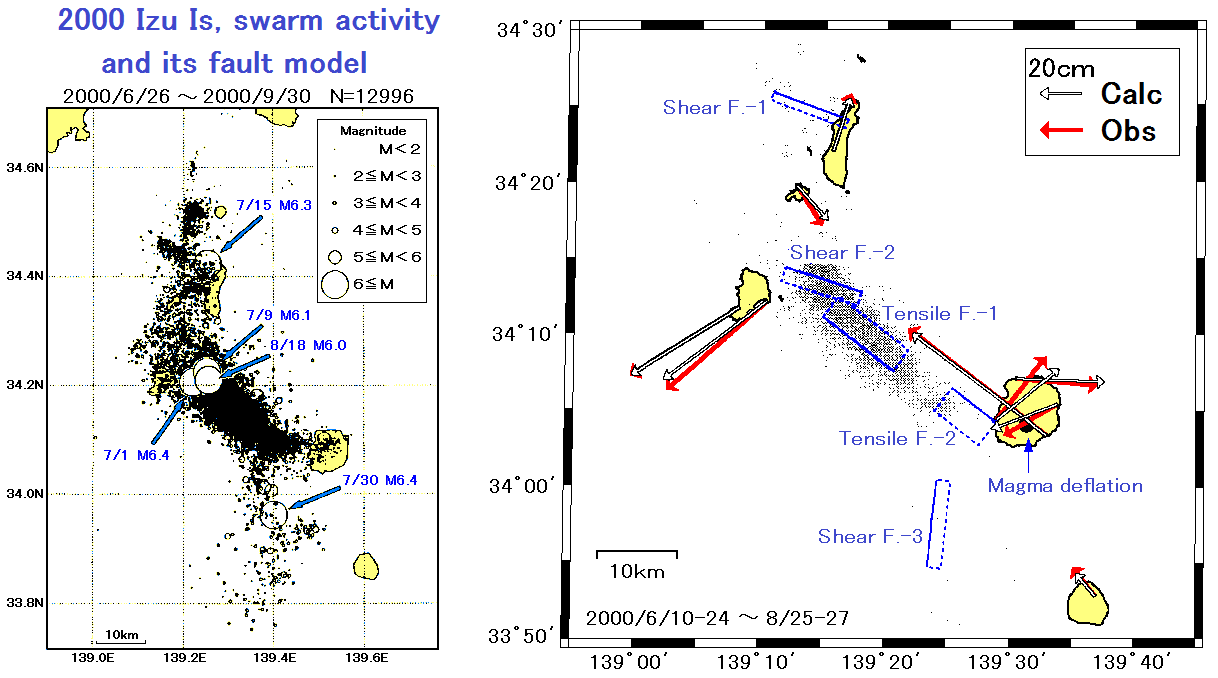
(例4) 2000年伊豆諸島群発地震
2000年6月末に始まった三宅島の火山活動は、その後、新島・神津島周辺海域に及ぶ大規模な群発地震活動に発展し、大きな地殻変動を伴いましたが、これら一連の活動は、Okada (1985)による理論式を用いて、複数の開口断層とずり断層の組合せによってモデル化されました[村上ほか(2001),月刊地球, 23, 791-800]。
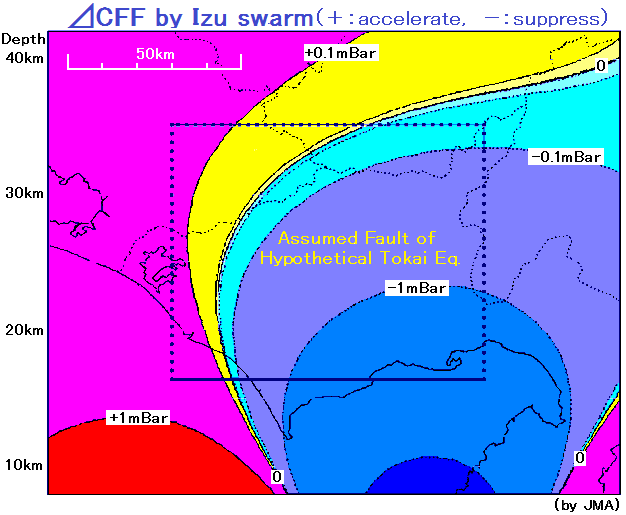
この激しい群発地震活動が、懸念される「東海地震」の発生にどのような影響を与えるかが憂慮されたため、上記のモデルによって東海地震の想定断層面上に及ぼすCFF(クーロン破壊関数)の変化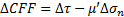 (
(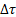 :ずり応力変化、
:ずり応力変化、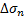 :法線応力変化、
:法線応力変化、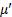 :実効摩擦係数)が、Okada (1992)による内部変形の式を用いて評価されました(気象庁資料,2000/9/1)。
:実効摩擦係数)が、Okada (1992)による内部変形の式を用いて評価されました(気象庁資料,2000/9/1)。
その結果、これらの地震により生じる応力変化は、日々繰り返される潮汐現象による応力の数分の1程度であり、直接的な影響はないであろうとの判断がなされました。
(例5) 2000年鳥取県西部地震
2000年10月6日に発生した鳥取県西部地震(M7.3)では、震源断層に沿った場所以外に、東西の約20km離れた位置でも顕著な余震活動が発生し、注目されました。
右の図は、本震周辺の地下8kmのレベルにおいて、本震と同じタイプの地震を起こす「ずり応力」がどのように分布するかを、Okada(1992)による内部変形の式を用いて計算したものです[遠田(2002), 地学雑誌, 111, 233-247]。
暖色系で示される地域では断層がすべり易くなり、寒色系の地域ではすべりにくくなることを示しています。震源から離れた東西の余震活動は「ずり応力」が増加した地域に一致しており、本震による応力変化によってトリガーされたものと解釈されました。このように、大きな地震のあとで余震が発生しやすい場所と、しにくい場所とを識別することができるようになりつつあります。

(例6) 2004年スマトラ島沖地震
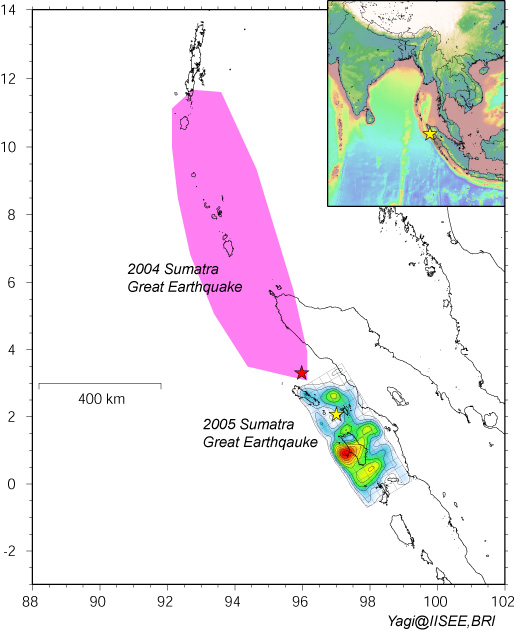
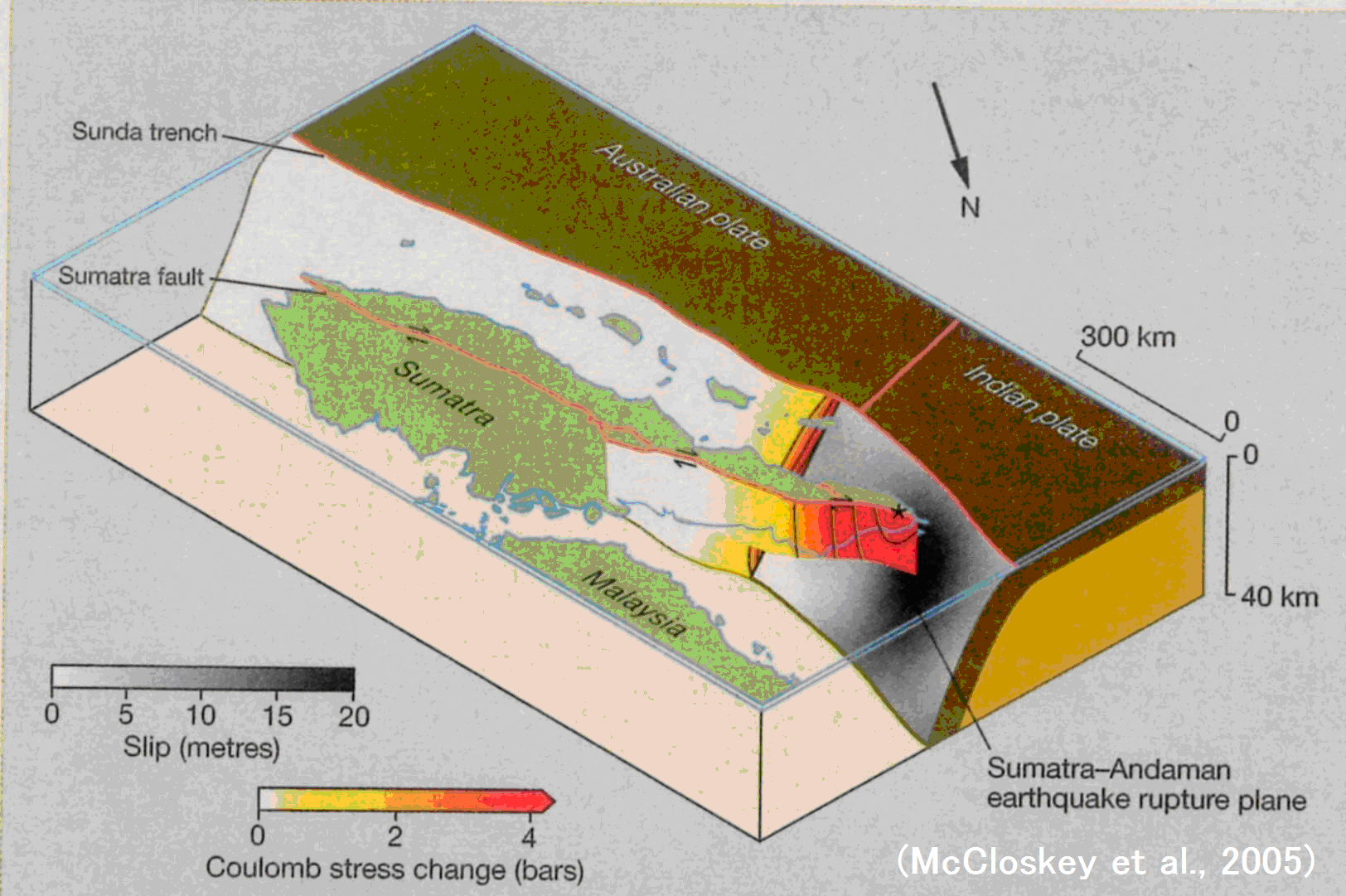
2004年12月26日に発生したスマトラ島沖地震(M9.1)はインド洋に大津波を起こし、数10万人もの犠牲者を出しましたが、その約3ヶ月後の2005年3月28日、すぐ東隣りのニアス島付近で再びM8.7の大地震が誘発されました(右図は、八木による両地震の震源域を示す)。
このような地震が誘発される可能性は、3月17日に発行された科学雑誌NATUREの中で事前に指摘されていました[McCloskey et al. (2005), Nature, 434, 291]。このような推論は、スマトラ島沖地震の発生によって周辺に生じる応力場をOkada(1992)による内部変形の式を用いて評価した結果、得られたものです。
(例7) 2011年東北地方太平洋沖地震
2011年3月11日に発生した東北地方太平洋沖地震(M9.0)では、巨大な津波により2万人近い死者・行方不明者を生じました。この地震により,東日本では広域にわたって非常に大きな地殻変動を生じ、周辺の広い範囲において活発な余震活動が続きました。
このように巨大な地震の発生は、近隣地域での地震や火山噴火など、様々な地学現象を誘発することが懸念されます。
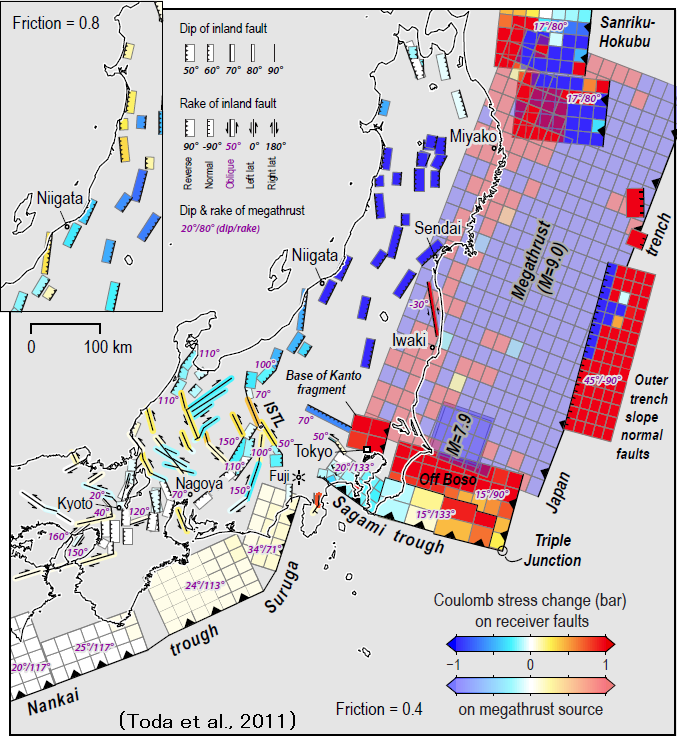
下の図は、Okada (1992)による内部変形の式を用いて、周辺海域での海溝型地震や内陸の活断層型地震に及ぼすCFF(クーロン破壊関数)の変化を評価した結果です[Toda et al. (2011), Earth Planets Space, 63, 725-730]。
暖色系で示される海域や活断層では地震の発生が促進され、寒色系の海域や活断層では地震の発生が抑制されることを示しています。
5 解説
DC3D0 / DC3D の基となった論文[Okada (1985), Okada (1992)]は、地震における断層運動のモデルとして使用される「ずり断層」、および火山における岩脈貫入のモデルとして使用される「開口断層」を統一的に扱い、地球表面および内部がどのように変形するかを計算する、もっとも一般的でかつ表現の簡潔な理論式を導出したものです。
地震および火山現象による地球変形の定式化は、以下のような手順で行われます。
地震や火山の源として、地中のある面を境とする変位の食い違いを考える「食い違いの弾性論」はSteketee (1958) により提唱され、その基本式は以下の通りです。
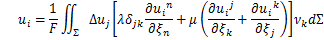
ここで、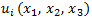 は観測点
は観測点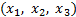 における変位ベクトル、
における変位ベクトル、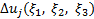 は面
は面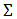 上での変位食い違いベクトル、
上での変位食い違いベクトル、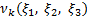 は面
は面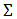 の法線ベクトル、
の法線ベクトル、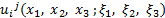 は面
は面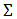 上の点
上の点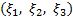 に置かれた
に置かれた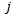 方向の力
方向の力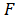 による媒質中の点
による媒質中の点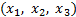 における変位の
における変位の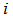 成分であり、
成分であり、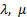 は媒質の弾性定数です。
は媒質の弾性定数です。
実際に上記の基本式を現実の問題に適用するためには、次の2つのアプローチがあります。
(1) コンピューターを用いて上記の積分計算を数値的に(力まかせで)行う。
(2) 上記の積分を数学的に行って、直接的な表現式(解析解)を導出する。
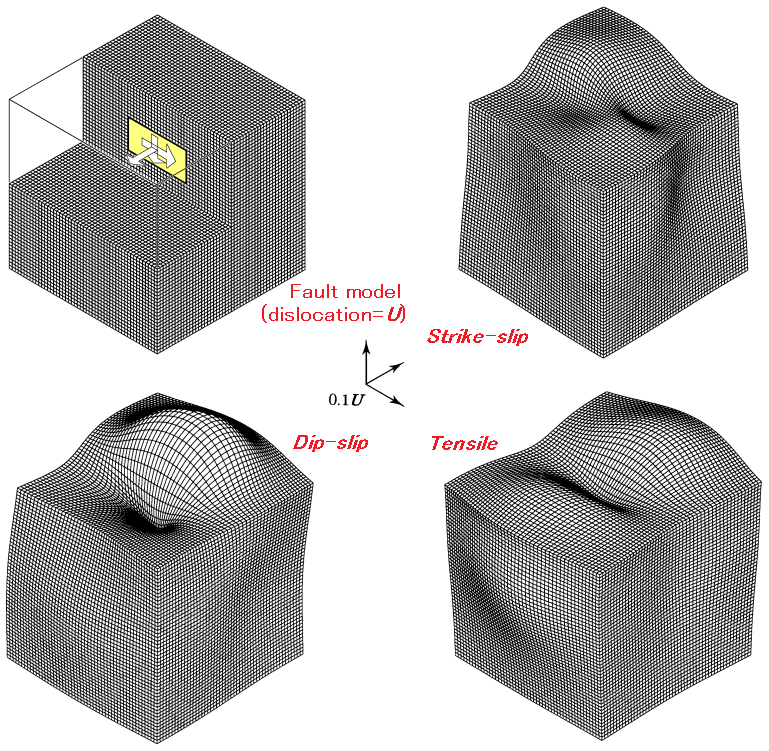
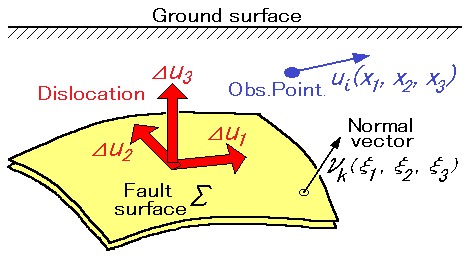
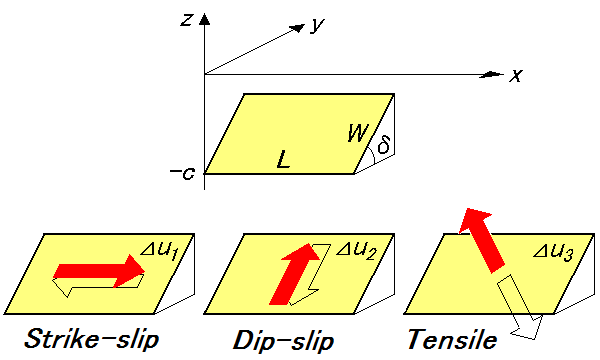
原理的には、(2)の方が計算誤差の入り込む余地がなく、(1)よりも遥かに迅速で正確な答が得られます。このため、これまで多くの研究者によって、具体的な断層モデル(下図)に対する地球表面や内部における変形を計算するための理論式が提出されてきました。
数学的な困難さを避けるため、当初は、媒質としてポアソン固体(上記の弾性定数の値が等しい場合)を仮定し、かつ断層面が垂直や水平な場合などの簡単なケースについて表現式が与えられました。
その後、徐々に一般的な場合に適用できる理論式が提出されてきましたが、その大部分は地震のモデルとしての「ずり断層」を対象としており、火山のモデルとしての「開口断層」についてはあまり研究が行われてきませんでした。
このため、すべての場合に適用できる完全な一般解は提出されておらず、また、過去の理論式の中には、最終的に同じ結果を与えるとはいえ、何ページにもわたるような非常に冗長な表現式を与えている場合も少なくありませんでした。
Okada (1985)およびOkada (1992)は、それまでバラバラに取り組まれてきた地震と火山のモデルを統一し、完全に一般的な形で、どんな断層モデルにも適用できるごく簡潔で美しい表現式を提出したものです。この結果は、IASPEI(国際地震学・地球内部物理学協会)の100周年記念号(2003年)に収録された用語集に「Okada model」として掲載され、当該分野の標準モデルとして国際的に広く認知されるようになりました。
DC3D0 / DC3D は、地震・火山現象をモデル化する際の標準的な道具として、また特定の地震や火山現象が周囲にどのような影響を及ぼすかを評価するための強力な道具として用いられており、本成果を発表した論文は地震や火山に関係する国内外の学術雑誌において最もよく引用される論文のひとつとなっています。なお2006年には、この功績が「地殻変動の定量的推定モデルの開発」として紫綬褒章を拝受する対象となりました。
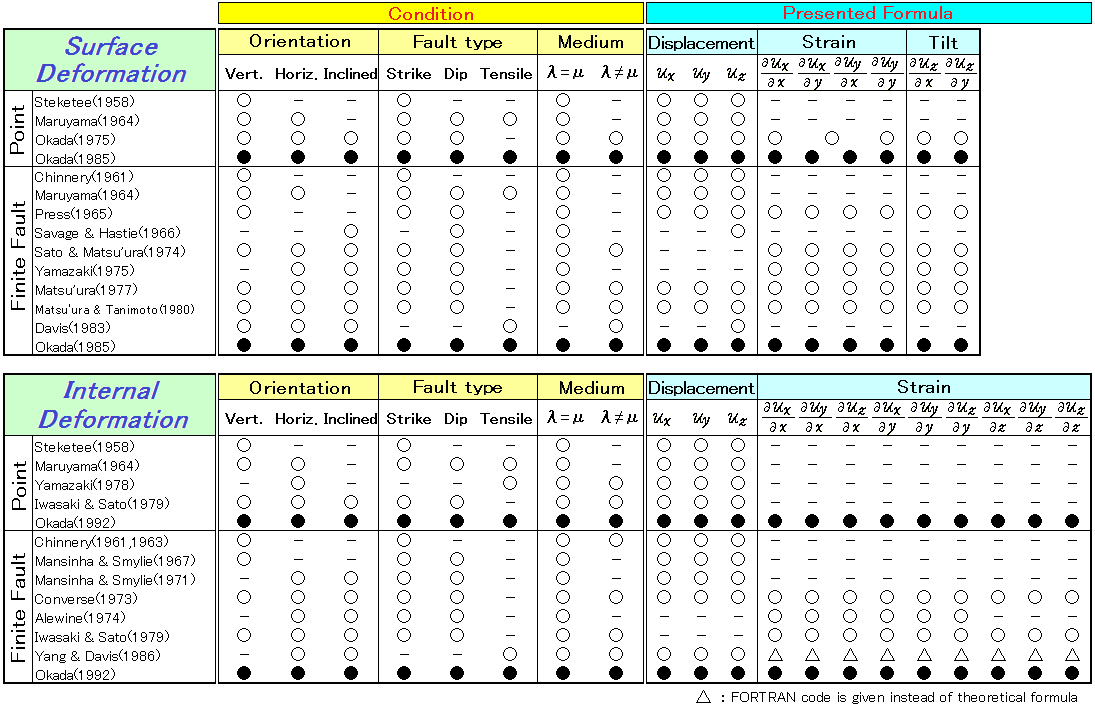
(1) これまでに提出された地表変形および内部変形の理論式
断層モデルには、その断層面の向き(垂直,水平,斜め)や断層運動の型(横ずれ,縦ずれ,開口)によって色々なタイプがあり、また媒質としては、弾性定数が等しい場合(ポアソン固体)と任意の場合とがあります。さらに、計算すべき物理量としては、地表変形の場合、変位3成分・歪4成分・傾斜2成分、内部変形の場合、変位3成分・歪9成分が必要です。
従来、これらのすべてを網羅する完全に一般的な表現式はありませんでしたが、Okada (1985)およびOkada (1992)によって,断層面の向き・断層運動の型・媒質を選ばず、かつすべての物理量を計算できる一般的な理論式のセットが提出されました(詳細については,§1プログラム概要にある参考論文を参照してください)。
(2) 断層モデルによる地表変形の理論式 (Okada, 1985)
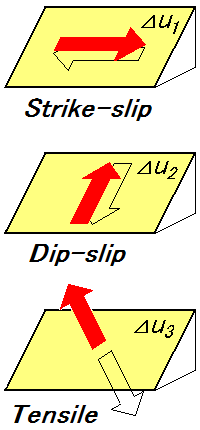
Strike-slip, Dip-slip, Tensile fault による表現式に統一感があり、全体として非常に簡潔かつ美しい表現式となっている点が特徴です。

(3) 断層モデルによる内部変形の理論式 (Okada, 1992)
本来であれば非常に複雑となる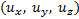 の計算式を、以下の
の計算式を、以下の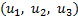 に変換することで簡潔なものとし、かつ全体を一枚の表形式でコンパクトに表現した点が大きな特徴です(詳細については、2ダウンロードにある「Derivation of Table6」を参照してください)。
に変換することで簡潔なものとし、かつ全体を一枚の表形式でコンパクトに表現した点が大きな特徴です(詳細については、2ダウンロードにある「Derivation of Table6」を参照してください)。

(4) 従来の表現式との比較例 (その1 : 縦ずれ断層,開口断層による上下変位成分)
縦ずれ断層による地表上下変位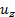 については、ポアソン媒質(
については、ポアソン媒質(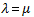 )の場合の式が Savage and Hastie (1966) により、また、開口断層による地表上下変位については、任意媒質(
)の場合の式が Savage and Hastie (1966) により、また、開口断層による地表上下変位については、任意媒質(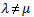 )の場合の式が Davis (1983) により提出されています。
)の場合の式が Davis (1983) により提出されています。
これら従来の表現式とOkada (1985)の式が数学的に等価であることは証明済みです。また、両者は数値的にも同一の結果を与えることを確認しています。Okada (1985)の式には統一性があり、かつ、はるかにコンパクトな表現式となっていることがわかります。

(5) 従来の表現式との比較例 (その2 : 横ずれ断層による水平歪成分)
横ずれ断層による地表水平歪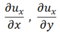 については、ポアソン媒質(
については、ポアソン媒質(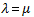 )の場合の式が 山崎(1975) により提出されています。こちらについても、従来の表現式とOkada (1985)の式が数学的に等価であることは証明され、また、両者は数値的にも同一の結果を与えることを確認しています。Okada (1985)の式ははるかにコンパクトな表現式となっていることがわかります。
)の場合の式が 山崎(1975) により提出されています。こちらについても、従来の表現式とOkada (1985)の式が数学的に等価であることは証明され、また、両者は数値的にも同一の結果を与えることを確認しています。Okada (1985)の式ははるかにコンパクトな表現式となっていることがわかります。

PDFファイルをご覧いただくには、アドビシステムズ社が配布しているAdobe Reader(無償)が必要です。Adobe Readerをインストールすることにより、PDFファイルの閲覧・印刷などが可能になります。
Adobe Readerのダウンロード
